Segundo Taller de Investigación

Presentaremos el segundo taller de investigación de Algoritmos y Estructuras de Datos II.
Nuestro tema elegido es Aplicación de estrategias de recorrido de grafos en la vida real (kruskal, prim, floyd-warshall y dijkstra).

Un Grafo es un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. 
Se puede decir entonces que un grafo es la representación gráfica de los datos de una situación particular.

Recorrido de un Grafo

Recorrer un grafo significa tratar de alcanzar todos los nodos que estén relacionados con uno que llamaremos nodo de salida. Existen básicamente dos técnicas para recorrer un grafo: recorrido por amplitud y recorrido por profundidad.

Teoría de Grafos

Es una rama de las matemáticas y las ciencias de la computación que estudia las propiedades de los grafos. Fue formulada por Leonhard Euler en 1736 con el problema de los puentes de Konisberg, donde se plantea la problemática de partir y llegar al mismo lugar recorriendo 7 puentes una única vez.

Actualmente ha tenido mayor preponderancia en el campo de la informática, las ciencias de la comunicación y las telecomunicaciones. Las aplicaciones de la teoría de grafos en la actualidad son numerosas, crecen día a día y se encuentran en campos tan diversos como la logística, traductores de idiomas, diseño de redes, optimización en investigación operativa, desarrollo de sensores en robótica, genética, entre otros.

Esta teoría transforma problemas de la vida real en problemas abstractos utilizando líneas y puntos.

Gracias a la teoría de grafos se pueden resolver diversos problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o sistemas de apertura, el diseño de líneas telefónicas, líneas de televisión por cable, el transporte colectivo o del metro, circuitos eléctricos de nuestras casas, etc.

También ayuda a resolver problemas más complejos como encontrar el camino más corto entre dos puntos, diseñar una red eléctrica de manera que el coste de diseño sea el más económico posible, orientar de forma adecuada las carreteras de una ciudad, etc.

Algoritmo de Kruskal

Es un algoritmo que sirve para encontrar un árbol de expansión mínimo en un grafo conexo y ponderado. Es decir, busca un subconjunto de aristas que, formando un árbol, incluyen todos los vértices y donde el valor de la suma de todas las aristas del árbol es el mínimo. Si el grafo no es conexo, entonces busca un bosque expandido mínimo (un árbol expandido mínimo para cada componente conexa).

El objetivo del algoritmo de Kruskal es construir un árbol (subgrafo sin ciclos) formado por arcos sucesivamente seleccionados de mínimo peso a partir de un grafo con pesos en los arcos.

El procedimiento consiste en elegir en forma arbitraria cualquier nodo y conectarlo con el más próximo de menos distancia o costo. Luego identificar el nodo no conectado que está más cerca o menos cuesta de alguno de los nodos conectados. Deshacer los empates de forma arbitraria. Finalmente se repite este paso hasta que se hayan conectado todos los nodos.

Aplicación del algoritmo de Kruskal en un problema de la vida real:

Este algoritmo puede ser utilizado en muchos campos como lo son las carreteras, vías férreas, aéreas o marítimas. También en redes eléctricas o de telefonía.

Actualmente empresas con servicios de cable e internet que necesitan expandirse lo más posible por toda una ciudad, hacen uso de estos algoritmos para seleccionar  las rutas cuyos caminos sean los más cortos y que generen un ahorro en el uso de cable como la fibra óptica.

Un ejemplo simple imaginable sería el querer viajar en auto por carretera a ciertas ciudades y buscar los caminos que generan distancias más cortas entre ciudades, en el menor tiempo posible o viajando la mínima cantidad de horas.

Algoritmo de Prim

Es un algoritmo perteneciente a la teoría de los grafos para encontrar un árbol recubridor mínimo en un grafo conexo, no dirigido y cuyas aristas están etiquetadas. El algoritmo incrementa continuamente el tamaño de un árbol, comenzando por un vértice inicial al que se le van agregando sucesivamente vértices cuya distancia a los anteriores es mínima.

El procedimiento consiste en seleccionar cualquier nodo y conectarlo con el más próximo que contenga el arco de menor costo o distancia. Se completa la red identificando el nodo no conectado que está más cerca o menos costoso de algunos de los nodos conectados. Luego se agrega este nodo al conjunto de nodos conectados. En caso de empate este se rompe en forma arbitraria.

Aplicación del algoritmo de Prim en un problema de la vida real:

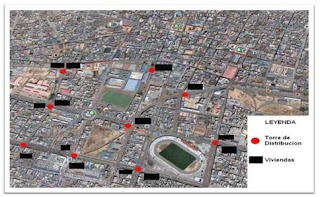
Situación: Implementación del cableado para el servicio de televisión por cable en ciertos puntos de un sector de la ciudad de Puno.

Problema: Ahorrar la mayor cantidad de cable (recursos) en los puntos estratégicos (torres de distribución) para llegar a todos los destinos deseados.

Datos: Distancia entre torres y casas es de 10 metros (cada casa)

Planteamiento: Se observa la ubicación de las torres de distribución y las viviendas.

Transformamos el conjunto de torres y viviendas en un Grafo.

Aplicamos el Algoritmo de Prim en el grafo para hallar el árbol recubrir mínimo o en otras palabras la ruta óptima para ahorra la distancia del cableado.

Algoritmo de Floyd-Warshall

Es un algoritmo de análisis sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El algoritmo encuentra el camino más corto entre todos los pares de vértices en una única ejecución.

Esto es semejante a construir una tabla con todas las distancias mínimas entre pares de ciudades de un mapa, indicando además la ruta a seguir para ir de la primera ciudad a la segunda. Este algoritmo es un ejemplo de programación dinámica.

Muchos problemas de la vida cotidiana se pueden expresar e incluso resolver en forma de grafo. Existen algoritmos que encuentran distintos tipos de soluciones, tanto booleanas como de eficiencia. El grafo se representa en una tabla (matriz) que se conoce como “matriz de adyacencia” y representa si existe una unión entre dos nodos.

Este algoritmo trabaja con grafos ponderados, es decir que el valor de la “flecha” que representamos en la matriz puede ser cualquier entero que se nos ocurra, o infinito, el cual marca que no existe unión entre los nodos. El resultado será una matriz donde estarán representadas las distancias mínimas entre nodos, seleccionando los caminos más convenientes según su ponderación o “peso”.

Los pasos a seguir son:

1. Hacer la tabla de ponderaciones, teniendo en cuenta que la diagonal principal debe ser nula. Se llena la tabla dependiendo de los adyacentes que tenga cada nodo. Si no se puede llegar directo a otro nodo se dice que es infinito.
2. Hacer la tabla de recorridos. En esta tabla se coloca el nombre del vértice en toda su columna.
3. Tomamos cada fila con cada columna de un vértice de nuestra tabla de ponderaciones. Sumamos cada dato y si el resultado es menor cambiamos el dato que se encuentra en esa posición. Cuando se modifica un dato en la tabla de ponderaciones, también se modifica en la tabla de recorridos con el vértice que se está analizando. 

El resultado final será:

Aplicación del algoritmo de Floyd-Warshall en un problema de la vida real:

Este algoritmo se puede aplicar a multitud de problemas, incluyendo el diseño de circuitos, el diseño de rutas de transporte, aproximaciones al problema del viajante de comercio, o como base de otros algoritmos más complejos.

Este algoritmo se utiliza también para modelar trayectos como el de una línea de autobús a través de las calles de una ciudad, en el que podemos obtener caminos óptimos para el trayecto.

Algoritmo de Dijkstra

El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de los vértices en un grafo con pesos en cada arista.

La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene. El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de coste negativo.

Una de sus aplicaciones más importantes reside en el campo de la telemática, gracias a él, podemos resolver grafos con muchos nodos, los cuales serían muy complicados de hacer sin dicho algoritmo, encontrando así las rutas más cortas entre un origen y todos los destinos en una red.

Aplicación del algoritmo de Djikstra en un problema de la vida real:

En múltiples aplicaciones donde se aplican los grafos, es necesario conocer el camino de menor costo entre dos vértices dados:

• Distribución de productos a una red de establecimientos comerciales.
• Distribución de correos postales.
• Encontrar la ruta más cercana entre un punto y otro en una ciudad.

Por ejemplo, un representante comercial tiene que visitar n ciudades conectadas entre sí por carreteras; su interés previsible será minimizar la distancia recorrida (o el tiempo, si se pueden prever atascos). El grafo correspondiente tendrá como vértices las ciudades, como aristas las carreteras y la valuación será la distancia entre ellas.
Y, de momento, no se conocen métodos generales para hallar un ciclo de valuación mínima, pero sí para los caminos desde a hasta b, sin más condición.

El algoritmo de Dijkstra es muy útil tanto en ámbito matemático como en la vida real ya que en escenas reales puede ser utilizado para diferentes tipos de problemas como el diseño de rutas de autobús y mejorar el servicio en las líneas de cableado de luz o en las tuberías de agua haciendo a este algoritmo muy útil por su uso y aplicación.